The PAROC Framework and Software Platform[Click here to visit the PAROC Framework website] The presence of uncertainty in process systems is one of the key reasons for deviation from set operation policies. As these uncertainties realize themselves on different time scales such as on a control, scheduling or design level, an integrated, comprehensive approach to consider uncertainty is required. Here we present PAROC, an integrated framework and software platform for the optimization and advanced model-based control of process systems (see here for more details). The key idea of the procedure is to decompose this challenging problem into a series of steps, each of which is described in detail below. A schematic representation of this framework is shown below: 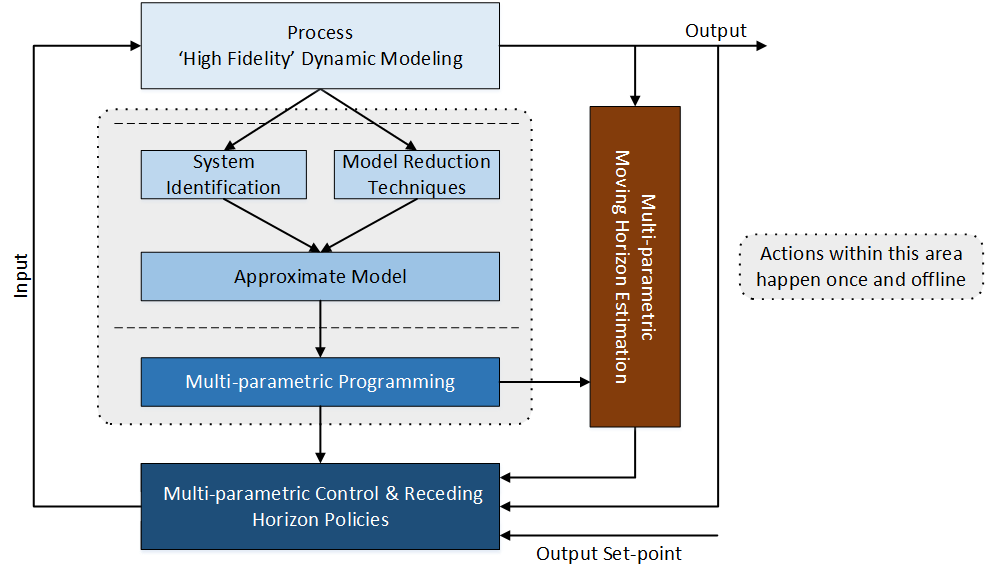
The interested reader is encouraged to check out the recently introduced PAROC App prototype in the PAROC website. Click here to directly download the App. Process 'High Fidelity' Dynamic ModelingThe first step of PAROC is the development of a 'high-fidelity dynamic model of the process. In particular, the scope is:
System Identification and Model Reduction TechniquesWhile it is possible to use the 'high-fidelity' model for design decisions, it is usually too complex in order to directly develop model-based strategies based on it. Consequently, it may be necessary to obtain a simplified version of the 'high-fidelity' model which retains the ability to follow the dynamic behaviour of the original model. In PAROC this is addressed using two different approaches. System IdentificationUsing a series of input-output simulations of the 'high-fidelity' model, statistical tools are used to generate an artificial, linear state-space which matches the output profile as closely as possible. This procedure has proven to be very powerful as it can be used by a user without having an advanced knowledge of the original system. One of the most widely used software tools for system identification is the System Identification toolbox by MATLAB®. Model Reduction TechniquesModel Reduction Techniques differ from system identification in two main aspects: First, they require less user interaction, as they somewhat 'automate' the generation of a reduced-order state-space model. Secondly, in some cases, the states generated by model reduction techniques have actual meaning in the original process. For recent advances in model reduction techniques, (see Lambert et al. (2013), Lambert et al. (2011), Lambert et al. (2013), Nascu et al. (2014), Rivotti et al. (2011) and Rivotti et al. (2012)). Multi-parametric Programming & Multi-parametric/explicit ControlAfter the approximate model has been obtained, the optimization problem to calculate the optimal receding horizon policies is formulated. In the case of model-based control, this results in the formulation of the model-predictive control (MPC) problem. In classical MPC, this problem is solved online as soon as the states of system are available. In PAROC, we use multi-parametric programming to calculate the explicit solution to the MPC problem offline. This reduces the online computational burden to a point location and a function evaluation (Bemporad et al., 2002). In multi-parametric programming, an optimization problem is not solved for a nominal point but for a range and as a function of bounded parameters. In general, the solution to this problem generates a partition of the considered parameter space, and each partition is associated with the corresponding optimal solution of the optimization problem as a function of parameters ((see ) for details on multi-parametric programming). Hence, in PAROC, the optimization problem, which is formulated based on the approximate model, is formulated as a multi-parametric programming problems where the states of the system, output setpoints and measured disturbances are treated as parameters. The optimization problem is then solved as a function thereof and the optimal solution consisting of the partitioning of the parameter space and the associated receding horizon policy as a function of the parameters considered. In the last step, this solution is connected to the 'high-fidelity' model and the developed policies are validated 'in-silico' in a closed-loop fashion. Multi-parametric Moving Horizon EstimationHowever, when solving the optimization problem in order to obtain the receding horizon policies it is assumed that the values of the parameters, i.e. amongst others the state vector, are exactly known. However, in real-world application this might not be the case, e.g. due to the presence of noise. Hence it becomes necessary to infer the state information from available output measurements using a state estimator. One long existing model-based technique for unconstrained state estimation is the Kalman filter. However, it does not provide the capability to explicitly handle constraints, a capability which is inherent to constrained estimation techniques such as the moving horizon estimator (MHE). In general, MHE is an estimation method that obtains these estimates by solving a constrained optimization problem given a horizon of past measurements. In PAROC, similarly to the calculation of the receding horizon policies, the MHE problem is solved in a multi-parametric fashion, where the past and current measurements and inputs and the initial guess for the estimated states are the parameters of the problem. Hence, the result of PAROC are two parametric solutions, namely the receding horizon policies as a function of the states of the system, output setpoints and measured disturbances and the states of the system, as a function of past and current measurements and inputs, and the initial guess for the estimated states. For details on multi-parametric moving horizon estimation, (see Lambert et al., 2013; Nascu et al., 2014). Closed-loop validationIn order validate the developed policies, the solution of the multi-parametric programming problem is tested in a closed-loop fashion in conjunction with the 'high-fidelity' model. Note that during this validation, no online optimization is performed, as only a point location and function evaluation is needed to obtain the optimal receding horizon policies. In case the simulation results are not satisfactory, the procedure of system identification or model reduction techniques and offline solution of the receding horizon policies is repeated. From a software perspective, this validation is carried out in PSE's gPROMS®, where the developed policies can be inserted from MATLAB® in a seamless fashion using custom-made software developed by our group. Hence, once the offline solution to the multi-parametric programming problems have been obtained in MATLAB®, the controller can be used directly in PSE's gPROMS®. |